James Beall
Principal Process Control Consultant
Today, I’ll share some guidance from the portion of the presentation on integrating processes. An example of an integrating process is a tank level. As you open the inlet and close the outlet to the tank, the level continues to rise.
James opened his discussion showing the first step to identify the open loop response. Like the self-regulating process example, it means to put the PID loop in manual mode and change the controller output. The process variable, PV, will begin to rise or fall based on the change. The process deadtime is the point at which the process variable stops its increase (or decrease) before switching directions.
The key parameters to capture are the % change in output (Δ%output), the initial slope of the PV (%/sec) before the output change, and the final slope of the PV (%/sec). The process gain, Kp is calculated by subtracting the initial slope from the final slope and then dividing the result by the Δ%output.
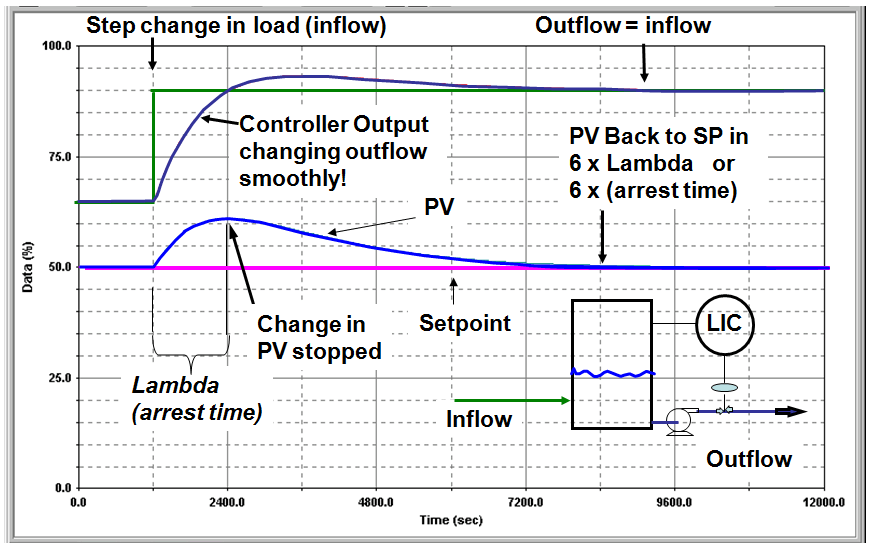
With the loop in automatic mode, the Lambda is defined as the time for the PV to cross the setpoint, SP, line after a change in the SP. The PV returns to SP in 6 Lambdas. For a changing load (load disturbance), such as an increase in the inflow to a tank, Lambda is point where the PV has stopped and is changing its direction. Lambda in this case is known as the arrest time. The PV returns to setpoint in 6 Lambdas or arrest times.James provided his Lambda tuning rules for integrating processes. He did not include dead time in the rules to keep the scope manageable. The reset time, Tr, is 2 * Lambda. The controller gain, Kc, is Tr / (Kp * Lambda2). Gain and reset time change with Lambda.
Often the purpose of tanks in a process is to absorb variability. In other words, the instead of trying to hold the level to a fixed height, the control strategy is to allow the level to swing in a range to absorb load changes in the process. Level control is the primary source of process capacity.
To tune level control for this situation you need to tune the controller only “fast” enough to hold the PV within the allowable level deviation (ALD) for a maximum load change. You want to choose the arrest time slow enough to provide for variability to maintain levels within the allowable variation. Lambda is a function of the allowable level variation / (integrating process gain, Kp * maximum load disturbance, MLD). You can find more detail in this earlier AIChE presentation by James.
If you’d like to learn more, James recommends three courses offered by Emerson Educational Services, Process Dynamics, Control and Tuning Fundamentals, Process Analysis and Minimizing Variability, and Modern Loop Tuning.
You can also connect with James and the Control Performance consultants to help with the specifics of your process control challenges.