Last year, some controversy broke out in the process automation and control community about the use of Lambda tuning for proportional-integral-derivative (PID)-based control. In a post, Lambda Tuning-Yeah or Neah?, we offered a differing view to a Control magazine article, The Case Against Lambda Tuning.

 Emerson’s Mark Coughran has written an excellent whitepaper that is located on the ControlGlobal.com website, Lambda Tuning — the Universal Method for PID Controllers in Process Control, to highlight the wide range of applications in which Lambda tuning can be applied.
Emerson’s Mark Coughran has written an excellent whitepaper that is located on the ControlGlobal.com website, Lambda Tuning — the Universal Method for PID Controllers in Process Control, to highlight the wide range of applications in which Lambda tuning can be applied.
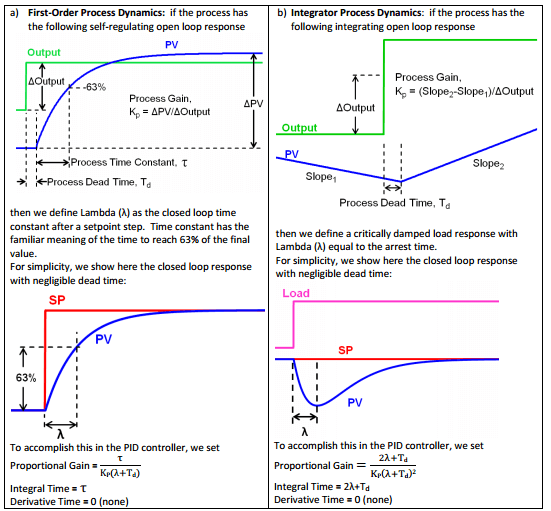
It provides a non-oscillatory response with the response time (Lambda or λ) required by the controlled process.
He opens noting six common process control challenges that automation professionals face. The first is with an oscillating control loop with the “as-found” tuning. These loops require a first-order setpoint response or critically damped load response. A Lambda (λ) value should be chosen that’s much greater than the process deadtime.
A second challenge is the need for minimum variability of the process variable (PV), which requires fast response of the control loop—shifting the variability to the output of the loop. A minimum robust λ should be at least 3X the process deadtime.
The third challenge is surge vessel applications that absorb process variability and need minimum variability on output. These require a slow response on the liquid level control loop unless a level limit is approached. λLEVEL should be as large as possible.
A fourth control challenge is a cascade PID loop configuration where the slave loop must respond faster than the master loop. λMASTER should be much greater than λSLAVE.
A fifth challenge is physically coupled or interacting processes, where the loop dynamics must be uncoupled. The Lambdas of the two loops should be set far apart from one another.
A final common control challenge is multiple streams into a blending vessel in which all inflows are required to respond at the same speed to inventory control. λFLOW A = λFLOW B = λFLOW N .
Mark notes that Lambda tuning provides a systematic and practical way to find the optimal tuning parameters to this wide range of challenges. He and his fellow Emerson consultants have accumulated 300 man-years of experience in applying the Lambda Tuning method, and have trained 3500 people on the method in paid training courses.
It’s important to use your common sense as a starting point with your knowledge of the plant, the purpose of the loop being controlled, potential interactions with other loops, and how the process responds to the controller (process dynamics).
Mark writes:
To comply with the production objectives of the plant, and to prevent interactions between loops, most loops need to respond in a certain amount of time. Learning which loops need to be fast and which need to be slow will make your tuning efforts more valuable to the plant. Finally, the process dynamics (MANUAL response) will limit how fast you can make the closed loop (AUTO) response.
Lambda tuning is related to Internal Model Control and Model Predictive Control and fits process dynamics including:
- First Order
- Integrator
- Integrator, First Order Lag
- Integrator, First Order Lead
- Integrator, Non-Minimum Phase
- Second Order, Overdamped
- Second Order, Underdamped
- Second Order, Lead
- Second Order, Lead with Overshoot
- Second Order, Non-Minimum-Phase
This picture shows Lambda tuning method for the two simplest and most common process responses:
Mark provides six great examples of the various challenges from different industries. These include:
- Closed loop flow rate control of Natural Gas Liquids through a control valve into a depropanizer column
- Pressure control of lubricating oil pumped from a reservoir to the propylene compressor of an olefins unit
- Level control in an oilfield produced water treatment tank
- Dissolved Oxygen (DO) control in a 2-liter bioreactor
- Reactor pressure control in the gasoline hydrotreater unit of a refinery
- Level control of Natural Gas Liquids in the surge tank that supplies a depropanizer column
You’ll want to read the whitepaper to see how Lambda tuning was applied to fit these very different applications and guidance on how to set the Lambda values to provide robust, non-oscillatory response.